Example problem: The spatially-adaptive solution of the azimuthally Fourier-decomposed 3D Helmholtz equation
In this document we discuss the spatially-adaptive finite-element-based solution of the 3D Helmholtz equation in cylindrical polar coordinates, using a Fourier-decomposition of the solution in the azimuthal direction.
The driver code is very similar to the one discussed in another tutorial – the main purpose of the current tutorial is to demonstrate the use of spatial adaptivity on unstructured meshes.
A specific example
We will solve the azimuthally Fourier-decomposed Helmholtz equation
![\[
\nabla^2 {u_{N}}(r,z) + \left(k^2-\frac{N^2}{r^2}\right) u_N(r,z) = 0,
\ \ \ \ \ \ \ \ \ \ \ \ (1)
\]](form_0.png)
where 
is the azimuthal wavenumber, in the finite domain 
. We impose the Sommerfeld radiation condition at the outer boundary of the computational domain at 
, using a Dirichlet-to-Neumann mapping, and apply flux boundary condition on the surface of the unit-sphere (where 
) such that the exact solution is given by
![\[
u_N(r,z)=u_N^{[exact]}(r,z)=\sum_{l=N}^{N_{\rm terms}}
h_{l}^{(1)}(k\sqrt{r^2+z^2}) \ P_{l}^{N}\left(\frac{z}{\sqrt{r^2+z^2}}\right).
\]](form_5.png)
This solution corresponds to the superposition of several outgoing waves that emerge from the unit sphere.
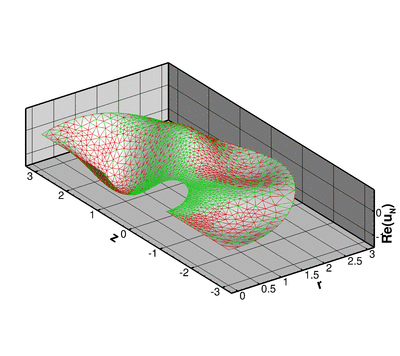
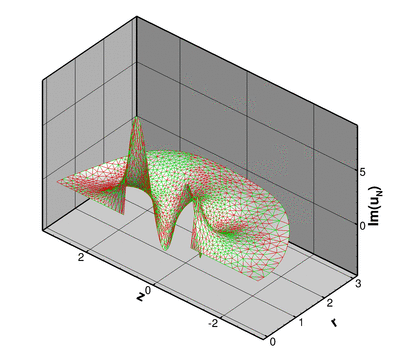
The two plots below show a comparison between the exact and computed solutions for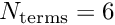 
, a Fourier wavenumber of 
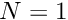, and a (squared) Helmholtz wavenumber of 
.
Plot of the exact (green) and computed (red) real parts of the solution of the Fourier-decomposed Helmholtz equation for N=1 and a wavenumber of k^2 = 10.
Plot of the exact (green) and computed (red) imaginary parts of the solution of the Fourier-decomposed Helmholtz equation for N=1 and a wavenumber of k^2 = 10.
The numerical solution
The driver code for this problem is very similar to the one discussed in another tutorial.
Running sdiff on the driver codes
and
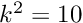shows the main differences required to discretise the computational domain with an adaptive, unstructured mesh:
- The provision of the functions
actions_before/after_adapt() to detach/re-attach theFaceElementsthat are used to enforce the Neumann boundary conditions before and after every spatial adaptation, and to pass the physical parameters to the newly created bulk elements.
- The generation of an unstructured mesh whose curvilinear boundaries are represented by
GeomObjects– this ensures that the domain boundaries become increasingly well resolved under mesh refinement.
That's all!
Code listing
Here's a listing of the complete driver code:
//LIC// ====================================================================
//LIC// This file forms part of oomph-lib, the object-oriented,
//LIC// multi-physics finite-element library, available
//LIC// at http://www.oomph-lib.org.
//LIC//
//LIC// Copyright (C) 2006-2025 Matthias Heil and Andrew Hazel
//LIC//
//LIC// This library is free software; you can redistribute it and/or
//LIC// modify it under the terms of the GNU Lesser General Public
//LIC// License as published by the Free Software Foundation; either
//LIC// version 2.1 of the License, or (at your option) any later version.
//LIC//
//LIC// This library is distributed in the hope that it will be useful,
//LIC// but WITHOUT ANY WARRANTY; without even the implied warranty of
//LIC// MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU
//LIC// Lesser General Public License for more details.
//LIC//
//LIC// You should have received a copy of the GNU Lesser General Public
//LIC// License along with this library; if not, write to the Free Software
//LIC// Foundation, Inc., 51 Franklin Street, Fifth Floor, Boston, MA
//LIC// 02110-1301 USA.
//LIC//
//LIC// The authors may be contacted at oomph-lib@maths.man.ac.uk.
//LIC//
//LIC//====================================================================
//Driver for Fourier-decomposed Helmholtz problem
#include <complex>
#include <cmath>
//Generic routines
#include "generic.h"
// The Helmholtz equations
#include "fourier_decomposed_helmholtz.h"
// The mesh
#include "meshes/triangle_mesh.h"
// Get the Bessel functions
#include "oomph_crbond_bessel.h"
using namespace oomph;
using namespace std;
/////////////////////////////////////////////////////////////////////
/////////////////////////////////////////////////////////////////////
/////////////////////////////////////////////////////////////////////
//===== start_of_namespace_planar_wave=================================
/// Namespace to test representation of planar wave in spherical
/// polars
//=====================================================================
namespace PlanarWave
{
/// Number of terms in series
unsigned N_terms=100;
/// Wave number
/// Imaginary unit
std::complex<double> I(0.0,1.0);
/// Exact solution as a Vector of size 2, containing real and imag parts
{
// Switch to spherical coordinates
double theta;
// Argument for Bessel/Hankel functions
// Need half-order Bessel functions
double bessel_offset=0.5;
// Evaluate Bessel/Hankel functions
double order_max_out=0;
// This function returns vectors containing
// J_k(x), Y_k(x) and their derivatives
// up to k=order_max, with k increasing in
// integer increments starting with smallest
// positive value. So, e.g. for order_max=3.5
// jv[0] contains J_{1/2}(x),
// jv[1] contains J_{3/2}(x),
// jv[2] contains J_{5/2}(x),
// jv[3] contains J_{7/2}(x).
kr,
// Assemble exact solution (actually no need to add terms
// below i=N_fourier as Legendre polynomial would be zero anyway)
complex<double> u_ex(0.0,0.0);
{
//Associated_legendre_functions
// Set exact solution
}
// Get the real & imaginary part of the result
}//end of get_exact_u
/// Plot
void plot()
{
unsigned nr=20;
unsigned nz=100;
unsigned nt=40;
{
Vector<double> x(2);
Vector<double> u(2);
{
{
}
}
}
}
}
/////////////////////////////////////////////////////////////////////
/////////////////////////////////////////////////////////////////////
/////////////////////////////////////////////////////////////////////
//===== start_of_namespace=============================================
/// Namespace for the Fourier decomposed Helmholtz problem parameters
//=====================================================================
namespace ProblemParameters
{
/// Square of the wavenumber
double K_squared=10.0;
/// Fourier wave number
int N_fourier=3;
/// Number of terms in computation of DtN boundary condition
unsigned Nterms_for_DtN=6;
/// Number of terms in the exact solution
unsigned N_terms=6;
/// Coefficients in the exact solution
/// Imaginary unit
std::complex<double> I(0.0,1.0);
/// Exact solution as a Vector of size 2, containing real and imag parts
{
// Switch to spherical coordinates
double theta;
// Argument for Bessel/Hankel functions
// Need half-order Bessel functions
double bessel_offset=0.5;
// Evaluate Bessel/Hankel functions
double order_max_out=0;
// This function returns vectors containing
// J_k(x), Y_k(x) and their derivatives
// up to k=order_max, with k increasing in
// integer increments starting with smallest
// positive value. So, e.g. for order_max=3.5
// jv[0] contains J_{1/2}(x),
// jv[1] contains J_{3/2}(x),
// jv[2] contains J_{5/2}(x),
// jv[3] contains J_{7/2}(x).
kr,
// Assemble exact solution (actually no need to add terms
// below i=N_fourier as Legendre polynomial would be zero anyway)
complex<double> u_ex(0.0,0.0);
{
//Associated_legendre_functions
// Set exact solution
}
// Get the real & imaginary part of the result
}//end of get_exact_u
/// Get -du/dr (spherical r) for exact solution. Equal to prescribed
/// flux on inner boundary.
{
// Initialise flux
flux=std::complex<double>(0.0,0.0);
// Switch to spherical coordinates
double theta;
// Argument for Bessel/Hankel functions
// Helmholtz wavenumber
// Need half-order Bessel functions
double bessel_offset=0.5;
// Evaluate Bessel/Hankel functions
double order_max_out=0;
// This function returns vectors containing
// J_k(x), Y_k(x) and their derivatives
// up to k=order_max, with k increasing in
// integer increments starting with smallest
// positive value. So, e.g. for order_max=3.5
// jv[0] contains J_{1/2}(x),
// jv[1] contains J_{3/2}(x),
// jv[2] contains J_{5/2}(x),
// jv[3] contains J_{7/2}(x).
kr,
// Assemble exact solution (actually no need to add terms
// below i=N_fourier as Legendre polynomial would be zero anyway)
complex<double> u_ex(0.0,0.0);
{
//Associated_legendre_functions
// Set flux of exact solution
}
}// end of exact_normal_derivative
} // end of namespace
/////////////////////////////////////////////////////////////////////
/////////////////////////////////////////////////////////////////////
/////////////////////////////////////////////////////////////////////
//========= start_of_problem_class=====================================
/// Problem class
//=====================================================================
template<class ELEMENT>
{
public:
/// Constructor
/// Destructor (empty)
/// Update the problem specs before solve (empty)
void actions_before_newton_solve(){}
/// Update the problem after solve (empty)
void actions_after_newton_solve(){}
/// Doc the solution. DocInfo object stores flags/labels for where the
/// output gets written to
/// Recompute gamma integral before checking Newton residuals
{
{
Helmholtz_outer_boundary_mesh_pt->setup_gamma();
}
}
/// Actions before adapt: Wipe the mesh of prescribed flux elements
void actions_before_adapt();
/// Actions after adapt: Rebuild the mesh of prescribed flux elements
void actions_after_adapt();
/// Check gamma computation
private:
/// Create BC elements on outer boundary
void create_outer_bc_elements();
/// Create flux elements on inner boundary
/// Delete boundary face elements and wipe the surface mesh
{
// Loop over the surface elements
{
// Kill surface element
}
// Wipe the mesh
boundary_mesh_pt->flush_element_and_node_storage();
}
#ifdef ADAPTIVE
/// Pointer to the "bulk" mesh
#else
/// Pointer to the "bulk" mesh
#endif
/// Pointer to mesh containing the DtN boundary
/// condition elements
/// on the inner boundary
/// Trace file
}; // end of problem class
//=====================start_of_actions_before_adapt======================
/// Actions before adapt: Wipe the mesh of face elements
//========================================================================
template<class ELEMENT>
{
// Kill the flux elements and wipe the boundary meshs
{
delete_face_elements(Helmholtz_outer_boundary_mesh_pt);
}
delete_face_elements(Helmholtz_inner_boundary_mesh_pt);
// Rebuild the Problem's global mesh from its various sub-meshes
}// end of actions_before_adapt
//=====================start_of_actions_after_adapt=======================
/// Actions after adapt: Rebuild the face element meshes
//========================================================================
template<class ELEMENT>
{
// Complete the build of all elements so they are fully functional
// Loop over the Helmholtz bulk elements to set up element-specific
// things that cannot be handled by constructor: Pass pointer to
// wave number squared
unsigned n_element = Bulk_mesh_pt->nelement();
{
// Upcast from GeneralisedElement to Helmholtz bulk element
//Set the k_squared pointer
el_pt->k_squared_pt() = &ProblemParameters::K_squared;
// Set pointer to Fourier wave number
el_pt->fourier_wavenumber_pt()=&ProblemParameters::N_fourier;
}
// Create prescribed-flux elements and BC elements
// from all elements that are adjacent to the boundaries and add them to
// Helmholtz_boundary_meshes
create_flux_elements_on_inner_boundary();
{
create_outer_bc_elements();
}
// Rebuild the Problem's global mesh from its various sub-meshes
}// end of actions_after_adapt
//=======start_of_constructor=============================================
/// Constructor for Fourier-decomposed Helmholtz problem
//========================================================================
template<class ELEMENT>
{
// Open trace file
Trace_file.open("RESLT/trace.dat");
// Create circles representing inner and outer boundary
double x_c=0.0;
double y_c=0.0;
double r_min=1.0;
double r_max=3.0;
// Edges/boundary segments making up outer boundary
//-------------------------------------------------
// Number of segments used for representing the curvilinear boundaries
unsigned n_segments = 20;
// All poly boundaries are defined by two vertices
// Bottom straight boundary on symmetry line
//------------------------------------------
boundary_vertices[0].resize(2);
boundary_vertices[0][0]=0.0;
boundary_vertices[0][1]=-r_min;
boundary_vertices[1].resize(2);
boundary_vertices[1][0]=0.0;
boundary_vertices[1][1]=-r_max;
unsigned boundary_id=0;
{
// Square outer boundary:
//-----------------------
boundary_vertices[0].resize(2);
boundary_vertices[0][0]=0.0;
boundary_vertices[0][1]=-r_max;
boundary_vertices[1].resize(2);
boundary_vertices[1][0]=r_max;
boundary_vertices[1][1]=-r_max;
boundary_vertices[2].resize(2);
boundary_vertices[2][0]=r_max;
boundary_vertices[2][1]=r_max;
boundary_vertices[3].resize(2);
boundary_vertices[3][0]=0.0;
boundary_vertices[3][1]=r_max;
boundary_id=1;
}
else
{
// Outer circular boundary:
//-------------------------
// The intrinsic coordinates for the beginning and end of the curve
boundary_id = 1;
}
// Top straight boundary on symmetry line
//---------------------------------------
boundary_vertices[0][0]=0.0;
boundary_vertices[0][1]=r_max;
boundary_vertices[1][0]=0.0;
boundary_vertices[1][1]=r_min;
boundary_id=2;
// Inner circular boundary:
//-------------------------
// The intrinsic coordinates for the beginning and end of the curve
boundary_id = 3;
// Create closed curve that defines outer boundary
//------------------------------------------------
// Use the TriangleMeshParameters object for helping on the manage of the
// TriangleMesh parameters. The only parameter that needs to take is the
// outer boundary.
// Specify maximum element area
double element_area = 0.1;
triangle_mesh_parameters.element_area() = element_area;
#ifdef ADAPTIVE
// Build "bulk" mesh
// Create/set error estimator
Bulk_mesh_pt->spatial_error_estimator_pt()=new Z2ErrorEstimator;
// Choose error tolerances to force some uniform refinement
Bulk_mesh_pt->min_permitted_error()=0.00004;
Bulk_mesh_pt->max_permitted_error()=0.0001;
#else
// Pass the TriangleMeshParameters object to the TriangleMesh one
#endif
// Check what we've built so far...
Bulk_mesh_pt->output("mesh.dat");
Bulk_mesh_pt->output_boundaries("boundaries.dat");
{
// Create mesh for DtN elements on outer boundary
Helmholtz_outer_boundary_mesh_pt=
// Populate it with elements
create_outer_bc_elements();
}
// Create flux elements on inner boundary
Helmholtz_inner_boundary_mesh_pt=new Mesh;
create_flux_elements_on_inner_boundary();
// Add the several sub meshes to the problem
add_sub_mesh(Bulk_mesh_pt);
add_sub_mesh(Helmholtz_inner_boundary_mesh_pt);
{
add_sub_mesh(Helmholtz_outer_boundary_mesh_pt);
}
// Build the Problem's global mesh from its various sub-meshes
// Complete the build of all elements so they are fully functional
unsigned n_element = Bulk_mesh_pt->nelement();
{
// Upcast from GeneralsedElement to the present element
//Set the k_squared pointer
el_pt->k_squared_pt()=&ProblemParameters::K_squared;
// Set pointer to Fourier wave number
el_pt->fourier_wavenumber_pt()=&ProblemParameters::N_fourier;
}
// Setup equation numbering scheme
} // end of constructor
//=================================start_of_check_gamma===================
/// Check gamma computation: \f$ \gamma = -du/dn \f$
//========================================================================
template<class ELEMENT>
{
// Compute gamma stuff
Helmholtz_outer_boundary_mesh_pt->setup_gamma();
char filename[100];
doc_info.number());
//first loop over elements e
unsigned nel=Helmholtz_outer_boundary_mesh_pt->nelement();
{
// Get a pointer to element
(Helmholtz_outer_boundary_mesh_pt->element_pt(e));
//Set the value of n_intpt
// Get gamma at all gauss points in element
Helmholtz_outer_boundary_mesh_pt->gamma_at_gauss_point(el_pt));
//Loop over the integration points
{
//Allocate and initialise coordiante
//Set the Vector to hold local coordinates
{
}
//Get the coordinates of the integration point
<< flux.real() << " "
<< flux.imag() << " "
<< std::endl;
}// end of loop over integration points
}// end of loop over elements
some_file.close();
}//end of output_gamma
//===============start_of_doc=============================================
/// Doc the solution: doc_info contains labels/output directory etc.
//========================================================================
template<class ELEMENT>
{
char filename[100];
// Number of plot points: npts x npts
unsigned npts=5;
// Output solution
//-----------------
doc_info.number());
some_file.close();
// Output exact solution
//----------------------
doc_info.number());
some_file.close();
// Doc error and return of the square of the L2 error
//---------------------------------------------------
doc_info.number());
Bulk_mesh_pt->compute_error(some_file,ProblemParameters::get_exact_u,
some_file.close();
// Doc L2 error and norm of solution
// Write norm of solution to trace file
Bulk_mesh_pt->compute_norm(norm);
Trace_file << norm << std::endl;
{
// Check gamma computation
check_gamma(doc_info);
}
} // end of doc
//============start_of_create_outer_bc_elements==============================
/// Create BC elements on outer boundary
//========================================================================
template<class ELEMENT>
{
// Outer boundary is boundary 1:
unsigned b=1;
// Loop over the bulk elements adjacent to boundary b?
{
// Get pointer to the bulk element that is adjacent to boundary b
//Find the index of the face of element e along boundary b
// Build the corresponding DtN element
//Add the flux boundary element to the helmholtz_outer_boundary_mesh
Helmholtz_outer_boundary_mesh_pt->add_element_pt(flux_element_pt);
// Set pointer to the mesh that contains all the boundary condition
// elements on this boundary
set_outer_boundary_mesh_pt(Helmholtz_outer_boundary_mesh_pt);
}
} // end of create_outer_bc_elements
//============start_of_create_flux_elements=================
/// Create flux elements on inner boundary
//==========================================================
template<class ELEMENT>
{
// Apply flux bc on inner boundary (boundary 3)
unsigned b=3;
// Loop over the bulk elements adjacent to boundary b
{
// Get pointer to the bulk element that is adjacent to boundary b
//Find the index of the face of element e along boundary b
// Build the corresponding prescribed incoming-flux element
//Add the prescribed incoming-flux element to the surface mesh
Helmholtz_inner_boundary_mesh_pt->add_element_pt(flux_element_pt);
// Set the pointer to the prescribed flux function
flux_element_pt->flux_fct_pt() = &ProblemParameters::exact_minus_dudr;
} //end of loop over bulk elements adjacent to boundary b
} // end of create flux elements on inner boundary
//===== start_of_main=====================================================
/// Driver code for Fourier decomposed Helmholtz problem
//========================================================================
{
// Store command line arguments
// Define possible command line arguments and parse the ones that
// were actually specified
// Square domain without DtN
CommandLineArgs::specify_command_line_flag("--square_domain");
// Parse command line
// Doc what has actually been specified on the command line
// Check if the claimed representation of a planar wave in
// the tutorial is correct -- of course it is!
//PlanarWave::plot();
// Test Bessel/Hankel functions
//-----------------------------
{
// Number of Bessel functions to be computed
unsigned n=3;
// Offset of Bessel function order (less than 1!)
double bessel_offset=0.5;
// Evaluate Bessel/Hankel functions
double x_min=0.5;
double x_max=5.0;
unsigned nplot=100;
{
double order_max_out=0;
// This function returns vectors containing
// J_k(x), Y_k(x) and their derivatives
// up to k=order_max, with k increasing in
// integer increments starting with smallest
// positive value. So, e.g. for order_max=3.5
// jv[0] contains J_{1/2}(x),
// jv[1] contains J_{3/2}(x),
// jv[2] contains J_{5/2}(x),
// jv[3] contains J_{7/2}(x).
{
}
bessely_file << std::endl;
{
}
besselj_file << std::endl;
{
}
bessely_deriv_file << std::endl;
{
}
besselj_deriv_file << std::endl;
}
bessely_file.close();
besselj_file.close();
bessely_deriv_file.close();
besselj_deriv_file.close();
}
// Test Legrendre Polynomials
//---------------------------
{
// Number of lower indices
unsigned n=3;
unsigned nplot=100;
{
{
}
some_file << std::endl;
}
some_file.close();
}
#ifdef ADAPTIVE
// Create the problem with 2D six-node elements from the
// TFourierDecomposedHelmholtzElement family.
#else
// Create the problem with 2D six-node elements from the
// TFourierDecomposedHelmholtzElement family.
#endif
// Create label for output
// Set output directory
doc_info.set_directory("RESLT");
// Solve for a few Fourier wavenumbers
{
// Step number
doc_info.number()=ProblemParameters::N_fourier;
#ifdef ADAPTIVE
// Max. number of adaptations
unsigned max_adapt=1;
// Solve the problem with Newton's method, allowing
// up to max_adapt mesh adaptations after every solve.
#else
// Solve the problem
problem.newton_solve();
#endif
//Output the solution
}
} //end of main
Definition sphere_scattering.cc:56
AnnularQuadMesh(const unsigned &n_r, const unsigned &n_phi, const double &r_min, const double &r_max, const double &phi_min, const double &phi_max)
Definition sphere_scattering.cc:65
void actions_after_adapt()
Actions after adapt: Rebuild the mesh of prescribed flux elements.
Definition unstructured_sphere_scattering.cc:437
void create_outer_bc_elements()
Create BC elements on outer boundary.
Definition sphere_scattering.cc:658
Mesh * Helmholtz_inner_boundary_mesh_pt
Mesh of face elements that apply the prescribed flux on the inner boundary.
Definition sphere_scattering.cc:426
void actions_after_newton_solve()
Update the problem after solve (empty)
Definition sphere_scattering.cc:394
void create_flux_elements_on_inner_boundary()
Create flux elements on inner boundary.
Definition sphere_scattering.cc:697
void actions_before_newton_solve()
Update the problem specs before solve (empty)
Definition sphere_scattering.cc:391
void doc_solution(DocInfo &doc_info)
Doc the solution. DocInfo object stores flags/labels for where the output gets written to.
Definition sphere_scattering.cc:574
void delete_face_elements(Mesh *const &boundary_mesh_pt)
Delete boundary face elements and wipe the surface mesh.
Definition unstructured_sphere_scattering.cc:373
FourierDecomposedHelmholtzDtNMesh< ELEMENT > * Helmholtz_outer_boundary_mesh_pt
Pointer to mesh containing the DtN boundary condition elements.
Definition sphere_scattering.cc:422
void actions_before_adapt()
Actions before adapt: Wipe the mesh of prescribed flux elements.
Definition unstructured_sphere_scattering.cc:418
void actions_before_newton_convergence_check()
Recompute gamma integral before checking Newton residuals.
Definition sphere_scattering.cc:401
Namespace to test representation of planar wave in spherical polars.
Definition sphere_scattering.cc:109
void get_exact_u(const Vector< double > &x, Vector< double > &u)
Exact solution as a Vector of size 2, containing real and imag parts.
Definition sphere_scattering.cc:121
Namespace for the Fourier decomposed Helmholtz problem parameters.
Definition sphere_scattering.cc:223
unsigned Nterms_for_DtN
Number of terms in computation of DtN boundary condition.
Definition sphere_scattering.cc:231
void exact_minus_dudr(const Vector< double > &x, std::complex< double > &flux)
Get -du/dr (spherical r) for exact solution. Equal to prescribed flux on inner boundary.
Definition sphere_scattering.cc:302
void get_exact_u(const Vector< double > &x, Vector< double > &u)
Exact solution as a Vector of size 2, containing real and imag parts.
Definition sphere_scattering.cc:243
int main(int argc, char **argv)
Driver code for Fourier decomposed Helmholtz problem.
Definition sphere_scattering.cc:732
Source files for this tutorial
- The source files for this tutorial are located in the directory:
demo_drivers/fourier_decomposed_helmholtz/sphere_scattering/
- The driver code is:
demo_drivers/fourier_decomposed_helmholtz/sphere_scattering/unstructured_sphere_scattering.cc
PDF file
A pdf version of this document is available. \