Public Member Functions | Protected Member Functions | List of all members
ComplexHarmonicEquations Class Referenceabstract

A class for all elements that solve the eigenvalue problem. More...

Inheritance diagram for ComplexHarmonicEquations:
QComplexHarmonicElement< NNODE_1D >

Public Member Functions

 ComplexHarmonicEquations ()
 Empty Constructor.
 
virtual double u (const unsigned &n) const
 Access function: First eigenfunction value at local node n Note that solving the eigenproblem does not assign values to this storage space. It is used for output purposes only.
 
virtual double w (const unsigned &n) const
 Second eigenfunction value at local node n.
 
void output (ostream &outfile)
 Output the eigenfunction with default number of plot points.
 
void output (ostream &outfile, const unsigned &nplot)
 Output FE representation of soln: x,y,u or x,y,z,u at Nplot plot points.
 
void fill_in_contribution_to_jacobian_and_mass_matrix (Vector< double > &residuals, DenseMatrix< double > &jacobian, DenseMatrix< double > &mass_matrix)
 Assemble the contributions to the jacobian and mass matrices.
 
double interpolated_u (const Vector< double > &s) const
 Return FE representation of function value u(s) at local coordinate s.
 
double interpolated_w (const Vector< double > &s) const
 Return FE representation of function value w(s) at local coordinate s.
 

Protected Member Functions

virtual double dshape_eulerian (const Vector< double > &s, Shape &psi, DShape &dpsidx) const =0
 Shape/test functions and derivs w.r.t. to global coords at local coord. s; return Jacobian of mapping.
 
virtual double dshape_eulerian_at_knot (const unsigned &ipt, Shape &psi, DShape &dpsidx) const =0
 Shape/test functions and derivs w.r.t. to global coords at integration point ipt; return Jacobian of mapping.
 
virtual int u_local_eqn (const unsigned &n, const unsigned &i)
 Access function that returns the local equation number of the unknown in the problem. Default is to assume that it is the first (only) value stored at the node.
 

Detailed Description

A class for all elements that solve the eigenvalue problem.

\[ \frac{\partial w}{\partial x} = \lambda u \]

\[ \frac{\partial u}{\partial x} = (\lambda - \mu) w \]

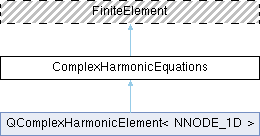
This class contains the generic maths. Shape functions, geometric mapping etc. must get implemented in derived class.

Definition at line 84 of file complex_harmonic.cc.

Constructor & Destructor Documentation

◆ ComplexHarmonicEquations()

ComplexHarmonicEquations::ComplexHarmonicEquations ( )
inline

Empty Constructor.

Definition at line 89 of file complex_harmonic.cc.

Member Function Documentation

◆ dshape_eulerian()

virtual double ComplexHarmonicEquations::dshape_eulerian ( const Vector< double > &  s,
Shape &  psi,
DShape &  dpsidx 
) const
protectedpure virtual

Shape/test functions and derivs w.r.t. to global coords at local coord. s; return Jacobian of mapping.

Implemented in QComplexHarmonicElement< NNODE_1D >.

◆ dshape_eulerian_at_knot()

virtual double ComplexHarmonicEquations::dshape_eulerian_at_knot ( const unsigned &  ipt,
Shape &  psi,
DShape &  dpsidx 
) const
protectedpure virtual

Shape/test functions and derivs w.r.t. to global coords at integration point ipt; return Jacobian of mapping.

Implemented in QComplexHarmonicElement< NNODE_1D >.

Referenced by fill_in_contribution_to_jacobian_and_mass_matrix().

◆ fill_in_contribution_to_jacobian_and_mass_matrix()

void ComplexHarmonicEquations::fill_in_contribution_to_jacobian_and_mass_matrix ( Vector< double > &  residuals,
DenseMatrix< double > &  jacobian,
DenseMatrix< double > &  mass_matrix 
)
inline

Assemble the contributions to the jacobian and mass matrices.

Definition at line 134 of file complex_harmonic.cc.

References dshape_eulerian_at_knot(), EigenproblemShift::Mu, u_local_eqn(), and w().

◆ interpolated_u()

double ComplexHarmonicEquations::interpolated_u ( const Vector< double > &  s) const
inline

Return FE representation of function value u(s) at local coordinate s.

Definition at line 224 of file complex_harmonic.cc.

References interpolated_u(), and u().

Referenced by interpolated_u(), interpolated_w(), and output().

◆ interpolated_w()

double ComplexHarmonicEquations::interpolated_w ( const Vector< double > &  s) const
inline

Return FE representation of function value w(s) at local coordinate s.

Definition at line 245 of file complex_harmonic.cc.

References interpolated_u(), and w().

Referenced by output().

◆ output() [1/2]

void ComplexHarmonicEquations::output ( ostream &  outfile)
inline

Output the eigenfunction with default number of plot points.

Definition at line 102 of file complex_harmonic.cc.

References output().

Referenced by output(), QComplexHarmonicElement< NNODE_1D >::output(), and QComplexHarmonicElement< NNODE_1D >::output().

◆ output() [2/2]

void ComplexHarmonicEquations::output ( ostream &  outfile,
const unsigned &  nplot 
)
inline

Output FE representation of soln: x,y,u or x,y,z,u at Nplot plot points.

Definition at line 110 of file complex_harmonic.cc.

References interpolated_u(), and interpolated_w().

◆ u()

virtual double ComplexHarmonicEquations::u ( const unsigned &  n) const
inlinevirtual

Access function: First eigenfunction value at local node n Note that solving the eigenproblem does not assign values to this storage space. It is used for output purposes only.

Definition at line 94 of file complex_harmonic.cc.

Referenced by interpolated_u().

◆ u_local_eqn()

virtual int ComplexHarmonicEquations::u_local_eqn ( const unsigned &  n,
const unsigned &  i 
)
inlineprotectedvirtual

Access function that returns the local equation number of the unknown in the problem. Default is to assume that it is the first (only) value stored at the node.

Definition at line 283 of file complex_harmonic.cc.

Referenced by fill_in_contribution_to_jacobian_and_mass_matrix().

◆ w()

virtual double ComplexHarmonicEquations::w ( const unsigned &  n) const
inlinevirtual

Second eigenfunction value at local node n.

Definition at line 98 of file complex_harmonic.cc.

Referenced by fill_in_contribution_to_jacobian_and_mass_matrix(), and interpolated_w().

The documentation for this class was generated from the following file: